A density curve gives us a good idea of the “shape” of a distribution, including whether or not a distribution has one or more “peaks” of frequently occurring values and whether or not the distribution is skewed to the left or the right. 2. A density curve lets us visually see where the mean and the median of a distribution are located. 3.
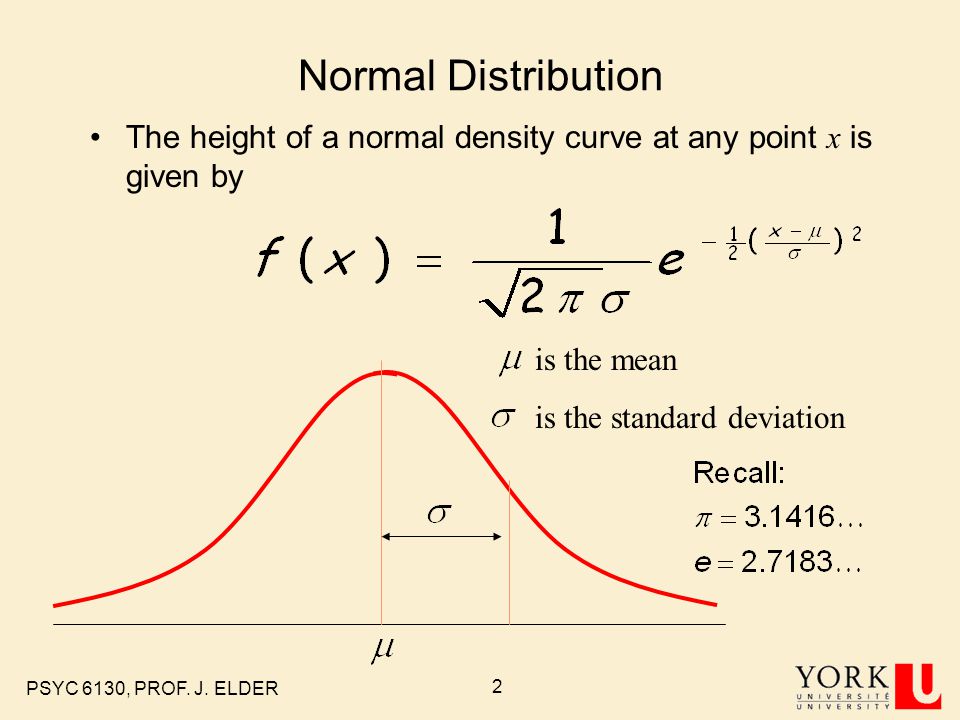
The Normal Distribution PSYC 6130, PROF. J. ELDER 2 is the mean is the standard deviation The height of a normal density curve at any point x is given. – ppt download
The density curve covers all possible data values and their corresponding probabilities. Hence the total area under the density curve will always be equal to 1. This area property of the density curve plays a crucial role in Statistics and Machine Learning. We’ll explore it further in the next post.

Source Image: medium.com
Download Image
0 1 is 1 (xfinal − xinitial = 1 − 0 = 1), so the height must also be 1. The density curve looks like the one at the right: We’re interested in values between 0.5 and 0.6.
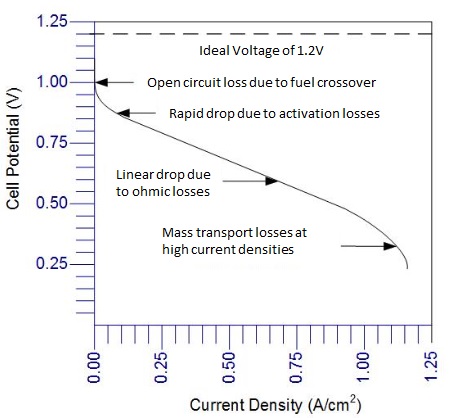
Source Image: fuelcellstore.com
Download Image
What are Density Curves? (Explanation & Examples) – Statology
Suppose we have the data : 10,10.5,11,17,19 and we map it into two intervals 10-15 and 15-20. So, the interval 10-15 will contain 3/5 data points and the interval 15-20 will contain 2/5 data points. Now if we calculate the area (as sum of areas of two rectangles), it comes out to be: area=3/5*5 + 2/5*5 =5 but not 1.
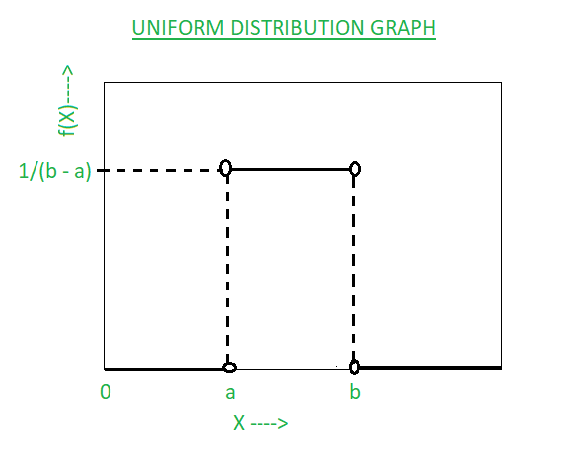
Source Image: geeksforgeeks.org
Download Image
What Height Must The Density Curve Have
Suppose we have the data : 10,10.5,11,17,19 and we map it into two intervals 10-15 and 15-20. So, the interval 10-15 will contain 3/5 data points and the interval 15-20 will contain 2/5 data points. Now if we calculate the area (as sum of areas of two rectangles), it comes out to be: area=3/5*5 + 2/5*5 =5 but not 1.
Like tossing a fair coin. In reality, we get fractions near 50%. BPS – 5th Ed. Chapter 3 4 Density Curves Always on or above the horizontal axis Have area exactly 1 underneath curve Area under the curve and above any range of values is the “theoretical” proportion of all observations that fall in that range BPS – 5th Ed. Chapter 3
Uniform Distribution Formula – GeeksforGeeks
Jul 21, 2022The area from the mean to z = – 1.58 is 0.44295. Subtracting this from 0.5, we get. P(z < − 1.58) = 0.5- 0.44295 = 0.05705. Doing this on the calculator, we must have both an upper and lower bound. Technically, though, the density curve does not have a lower bound, as it continues infinitely in both directions.
r – Scale density curve made with geom_density to similar height of geom_histogram? – Stack Overflow

Source Image: stackoverflow.com
Download Image
What are Norms? Understanding normative data – 2024 Edition – 2024 Edition – VALD Performance | Human Measurement Technologies
Jul 21, 2022The area from the mean to z = – 1.58 is 0.44295. Subtracting this from 0.5, we get. P(z < − 1.58) = 0.5- 0.44295 = 0.05705. Doing this on the calculator, we must have both an upper and lower bound. Technically, though, the density curve does not have a lower bound, as it continues infinitely in both directions.

Source Image: valdperformance.com
Download Image
The Normal Distribution PSYC 6130, PROF. J. ELDER 2 is the mean is the standard deviation The height of a normal density curve at any point x is given. – ppt download
A density curve gives us a good idea of the “shape” of a distribution, including whether or not a distribution has one or more “peaks” of frequently occurring values and whether or not the distribution is skewed to the left or the right. 2. A density curve lets us visually see where the mean and the median of a distribution are located. 3.
Source Image: slideplayer.com
Download Image
What are Density Curves? (Explanation & Examples) – Statology
0 1 is 1 (xfinal − xinitial = 1 − 0 = 1), so the height must also be 1. The density curve looks like the one at the right: We’re interested in values between 0.5 and 0.6.

Source Image: statology.org
Download Image
A Complete Guide to Histograms | Tutorial by Chartio
The area of a rectangle is height x width, so if you multiply the height x width in this case you would get .5 x 1 = .5. Add them together and you get .5 + .5 =1. If we add more bars to the graph, like in the example histogram below, we get something that’s starting to look like a curve. If you add up all of the areas of these rectangles
Source Image: chartio.com
Download Image
A Mathcad Utility Function for Air Pressure and Density | Math Encounters Blog
Suppose we have the data : 10,10.5,11,17,19 and we map it into two intervals 10-15 and 15-20. So, the interval 10-15 will contain 3/5 data points and the interval 15-20 will contain 2/5 data points. Now if we calculate the area (as sum of areas of two rectangles), it comes out to be: area=3/5*5 + 2/5*5 =5 but not 1.

Source Image: mathscinotes.com
Download Image
Create a Normal Distribution Curve in Google Sheets | Easy 2-min Guide – Amigo: No-code Data Integrations to Google Sheets
Like tossing a fair coin. In reality, we get fractions near 50%. BPS – 5th Ed. Chapter 3 4 Density Curves Always on or above the horizontal axis Have area exactly 1 underneath curve Area under the curve and above any range of values is the “theoretical” proportion of all observations that fall in that range BPS – 5th Ed. Chapter 3

Source Image: blog.tryamigo.com
Download Image
What are Norms? Understanding normative data – 2024 Edition – 2024 Edition – VALD Performance | Human Measurement Technologies
Create a Normal Distribution Curve in Google Sheets | Easy 2-min Guide – Amigo: No-code Data Integrations to Google Sheets
The density curve covers all possible data values and their corresponding probabilities. Hence the total area under the density curve will always be equal to 1. This area property of the density curve plays a crucial role in Statistics and Machine Learning. We’ll explore it further in the next post.
What are Density Curves? (Explanation & Examples) – Statology A Mathcad Utility Function for Air Pressure and Density | Math Encounters Blog
The area of a rectangle is height x width, so if you multiply the height x width in this case you would get .5 x 1 = .5. Add them together and you get .5 + .5 =1. If we add more bars to the graph, like in the example histogram below, we get something that’s starting to look like a curve. If you add up all of the areas of these rectangles